本ツールの技術的詳細
ダメージ計算式
ダメージはキャラクター自体のステータスと敵のステータスに左右されます. 元素反応ではないダメージに関係するキャラクター自体のステータスは次の通りです.
- 天賦レベルで決まる天賦倍率 $s$
- 攻撃力 $A$
- 会心率(ダメージ数値には影響しない) $C$
- 会心ダメージ(会心時のみ) $D$
- ダメージバフ $G_d$
また,ダメージに関連する敵のステータスは次の通りです.
- 元素耐性による減衰 $R$
- レベルによる減衰(敵の防御力) $L$
これらを用いると,原神における(元素反応ではない)ダメージは次の通り計算できます.
\[\begin{align*} \text{Damage w/o Crit.} &= sA(1 + G)RL\\ \text{Damage w/ Crit.} &= sA(1 + D)(1 + G)RL \end{align*}\]一行目は非会心時のダメージで,二行目が会心時のダメージです. 会心率$C$であれば,確率$C$で会心時のダメージとなり,確率$(1-C)$で非会心時のダメージとなります. 従って,ダメージ期待値は次のように計算できます.
\[\mathbb{E}[\text{Damage}] = sA(1 + CD)(1 + G)RL\]もちろん,キャラクターや武器によっては,HPを攻撃力に変換したり,攻撃力の代わりに防御力を参照してダメージを計算したりします. ただ,原神におけるダメージの多くはこの計算式に従いますので,この計算式のみを説明します. それでは,それぞれの項目を詳しく説明します.
天賦倍率 $s$
キャラクターの天賦ステータス詳細画面で「~のダメージ XXX%」と書いてある数値です. 天賦レベルによって決まります.
攻撃力 $A$
基本的には攻撃力は基礎攻撃力と倍率(攻撃力%)と加算値で決まり,攻撃力$A$は次のように計算されます.
\[A = (A_\text{b,c} + A_\text{b,w}) (1 + a_r) + A_\text{add}\]ここで各文字は次のとおりです.
- キャラクターの基礎攻撃力 $A_\text{b,c}$
- 武器の基礎攻撃力 $A_\text{b,w}$
- 累計倍率(攻撃力%) $a_r$
- 累計加算値 $A_\text{add}$
聖遺物の羽のように加算値(いわゆる実数値)は$A_\text{add}$に足され,攻撃力%はすべて$a_r$へ加算されます.
この中でもレベルによる減衰$L$は敵レベルと自身のレベルのみで決まるため,聖遺物や武器では$L$を変えることはできません.
ダメージバフ $G$
ゲーム中では「天賦倍率$s$と攻撃力$A$のみの積$sA$」をダメージと呼称しています. この値は実際に敵に与えられる(画面に表示される)ダメージとは異なりますが,たとえばポケモンでいえば「技の威力」がこれに当たると考えるとわかりやすいかと思います. この技の威力に対して,ダメージのバフや会心,相手による減衰の計算をすることで最終的なダメージが計算されます.
ダメージのバフの最も典型的な例がダメージバフと呼ばれているもので,たとえば聖遺物の杯の「~元素ダメージ」とか「物理ダメージ」などの数値がこれに当たります. たとえば,「ダメージ+30%」とは「ダメージ値$sA$に30%のボーナスを与える」という意味なので,ダメージ値が「$1.3 \times sA$」となります. 一般的にはダメージバフの累計値を$G$とすると,ダメージバフを考慮したダメージ値は$sA(1+G)$となります.
会心率$C$・会心ダメージ$D$
ダメージ計算式の中で唯一確率的な要素になっているのが会心系です. いわゆるクリティカルとか急所とか,そういう概念です. 会心率が$C$とは,確率$C$で会心が発生し,確率$(1-C)$で非会心であるという意味です. 非会心時のダメージを$X$とすると,会心時のダメージは$X(1+D)$になります. つまり,キャラクターの会心ダメージが100%とは,会心によってダメージが2倍になること意味します.
耐性による減衰 $R$
敵は各元素や物理に対して耐性を持っています. ヒルチャールなどの一般の敵は,すべての元素に対して一律に10%の耐性を持っています. 一方で,遺跡守衛系は物理に対して高い耐性を持っていたり,炎のトリックフラワーは炎元素への耐性が高くなっていたりします.
耐性値が$x$のとき,減衰量$R$は少し複雑な計算になります.
\[R = \begin{cases} \frac{1}{4x+1}, & x > 0.75 \\ 1 - x, & 0 < x \leq 0.75 \\ 1 - \frac{x}{2}, & x < 0 \end{cases}\]たとえば,元々の耐性が10%で,翠緑4セット効果で30%耐性が下がった場合は$x = 0.1 - 0.3 = -0.2$となります. このとき,耐性による減衰値は$R = 1 - \frac{-0.2}{2} = 1.1$となり,1.1倍になります(減衰どころか増加します).
レベルによる減衰 $L$
実は相手のレベルと自分のレベルによってダメージは変わります. この減衰量は次のように計算されます.
\[L^{-1} = 1 + \frac{1 + l_e}{1 + l_c} (1 - b_r)\]上の式では綺麗に記述するために,左辺が逆数$L^{-1}$になっていることに注意してください. ここで,$l_e$と$l_c$はそれぞれ敵と自身のレベルを100で割った値(90レベルなら0.9)です. また,$b_r$は敵の防御力を低下させる効果です(ちなみにこれとは別に「防御力を無視する効果」も存在します). もし,敵と自身のレベルが等しく($l_e = l_c$),防御力を低下させる効果がない($b_r = 0$)のであれば$L=1/2 = 0.5$となりダメージは半減します. 敵のレベルは高いほどに敵の防御力は高く,ダメージは低下します.
聖遺物サブステータスのスコア(コスト)計算式
最適化では,聖遺物のサブステータスに何らかの制約を設けて,その制約条件の元でダメージが最大になるようにサブステータスの配分を最適化します. 原神Wikiの記述によると,星5聖遺物のサブステータスの上昇量は以下の表の通りです.
| サブステ | 上昇量(中) |
|---|---|
| 攻撃力%($a$) | 4.7% |
| 防御力%($b$) | 5.8% |
| HP%($h$) | 4.7% |
| 会心率($c$) | 3.1% |
| 会心ダメージ($d$) | 6.2% |
| 元素チャージ効率($r$) | 5.2% |
| 元素熟知($m$) | 19 |
このため,スコア(コスト)計算式は次の通り設定しています.
\[\mathrm{cost}(\mathbf{x}) = \mathrm{cost}([a, b, h, c, d, r, m]) = 6.2\times \left(\frac{a}{0.047} + \frac{b}{0.058} + \frac{h}{0.047} + \frac{c}{0.031} + \frac{d}{0.062} + \frac{r}{0.052} + \frac{m}{19}\right)\]この数式の意味は,一般的によく使われている数式「攻撃力% + 会心率 $\times$ 2 + 会心ダメージ」をより厳密に一般化した数式であると認識していただくのが簡単でしょう. たとえばサブステータスにおいて攻撃力の4.7%の増加と会心ダメージの6.2%の増加のコストは同じであることを意味しています. もう少し言えば,コストの値を6.2で割った値が,聖遺物でサブステータスが上昇した回数を意味します(ただし,実際には上昇量には振れ幅があるので,現実上の聖遺物では成立しないことに注意してください). サブステータスの上昇回数には上限があるため,本サイトではこの計算式をコストとしています.
この計算式を制約とすることで,ユーザーは「聖遺物5つの合計スコア$S$において,ダメージが最大となるサブステータスの配分」を知ることができます. また,複数の武器や聖遺物セットを比較するとき,比較の前提として「聖遺物5つの合計スコア$S$において最適化されている」状態で比較できます. そのため,たとえば会心率が伸びる武器と会心ダメージが伸びる武器を比較したいときも,それぞれの最適な状態でステータス配分で比較できるため公平に比較できます.
また,本最適化サイトでは聖遺物の実質的なダメージへの影響度である聖遺物有効度と 聖遺物がどれだけ実現困難かの指標である聖遺物偏差値を利用しています. これらはスコア(コスト)計算とは異なる概念ですのでご注意ください.
最適化アルゴリズム
最適化したいダメージ計算式$f(\mathbf{x})$を最適化アルゴリズムを用いて最適化します. 最適化問題の定式化は以下のようになります.
\[\begin{align} &\text{maximize} &&f(\mathbf{x}) \\ &\text{subject to} &&\mathrm{cost}(\mathbf{x}) \leq S \\ & &&\mathbf{x}_i \geq 0, &\forall i \in \{0,1,\cdots,7\} \end{align}\]最後の制約$\mathbf{x}_i \geq 0$さえなければ,大学で習うラグランジュの未定乗数法で解けるのですが, 最後の制約$\mathbf{x}_i \geq 0$があるので少し厄介です.
目的関数$f(\mathbf{x})$が積の形になっているため,対数を取ることで通信の世界でよく用いられる注水定理が使えるかと考えてみましたが,たとえば会心率と会心ダメージの項は$(1 + cd)$と積になっていたり,HPを攻撃力に変換する効果があったりするので,少し難しそうだと思いました. それに,今後たとえば「攻撃力を会心率に変換する」なんていうトンデモ効果を持ったキャラや聖遺物が出てくる可能性も0ではない気がするので,もう少し柔軟に最適化する方法を考えました.
そのため,このサイトではnloptという汎用の非線形最適化ライブラリのJavascriptバインディングnlopt-jsを利用しています.
ただ,先程も記述した通り,目的関数$f(\mathbf{x})$が積の形になっているため,対数を取ることでより簡単な問題に変換できます. よって,以下の最適化問題をnloptを用いて最適化します.
\[\begin{align} &\text{maximize} &&\log f(\mathbf{x}) \\ &\text{subject to} &&\mathrm{cost}(\mathbf{x}) \leq S, \\ & &&\mathbf{x}[i] \geq 0, &\forall i \in \{0,1,\cdots,7\} \end{align}\]実際に開発の段階では,上記のように対数を用いることで局所最適解用のアルゴリズムでも大域最適解に落ち込む確率が大幅に増加し,安定して大域最適解へ落ちていることを確認しています.
単に対数を取るだけで簡単になるなんて不思議に思うかもしれませんが,たとえば次のような積の関数を考えてみましょう.
\[\begin{align} f(\mathbf{x}) = f([a, b]) = (1 + a)(1 + b) \end{align}\]この関数$f(\mathbf{x})$を$a,b$でそれぞれ偏微分すると以下のようになります.
\[\begin{align} \frac{\partial f}{\partial a} &= (1 + b) \\ \frac{\partial f}{\partial b} &= (1 + a) \\ \end{align}\]一方で,対数を取った目的関数とその偏微分は次のようになります.
\[\begin{align} \log f(\mathbf{x}) &= \log(1+a) + \log(1 + b) \\ \frac{\partial \log f}{\partial a} &= \frac{1}{1 + a} \\ \frac{\partial \log f}{\partial b} &= \frac{1}{1 + b} \\ \end{align}\]対数を取る前は$a$での偏微分の値が$b$に依存していますが,対数を取ると$a$での偏微分の値は$b$に依存しないことがわかります. 原神におけるダメージの最適化問題も先程の例のようにパラメータの積の形になっているため,同様の原理でより簡単に解けるようになります. もちろん,目的関数の対数をとってもいい理由は対数が単調増加関数なためです.
また,本サイトのプログラムでは,複雑なダメージ計算式を手で微分する手間を無くしたり柔軟性を向上させるために,いわゆる計算グラフの構築と自動微分(たとえばautogradのような)をする簡単なプログラムを組んでいます. このため,HPを攻撃力に変換したり,チャージ効率をダメージバフに変換するような効果があっても,人間が個別に数式を用意して微分する必要はありません. プログラムが各キャラや聖遺物セットに基づいたダメージの計算式を自動で構築して,そこからダメージ値$f(\mathbf{x})$と同時に勾配ベクトル(偏微分; $\nabla \log f(\mathbf{x})$)まで自動計算します.
ダメージ値と勾配ベクトルを用いて,実際に聖遺物のサブステータスを最適化するのはSLSQP(Sequential Least SQuares Programming)というアルゴリズムを使用します. このアルゴリズムは局所最適解を求めるためのアルゴリズムですが,今回の最適化問題においては開発時の段階では大体1ms以下で大域最適解にたどり着いており,今回の問題でも実用的であるといえます.
[Tips] どうして会心率と会心ダメージは1:2がベストなのか
簡素化したダメージ計算式を以下に示します. この計算式では攻撃力と会心系しかダメージ計算に含めていません. $A_\mathrm{b}$は基礎攻撃力,$a_b$は聖遺物以外での攻撃力%,$a$は聖遺物による攻撃力%,$A_\mathrm{add}$は聖遺物の羽のような攻撃力実数値,$c_b$は聖遺物以外での会心率,$c$は聖遺物による会心率,$d_b$は聖遺物以外での会心ダメージ,$d$が聖遺物での会心ダメージになります.
\[f(\mathbf{x}) = f([a, c, d]) = \{A_\mathrm{b} (1 + (a_b + a)) + A_\mathrm{add} \} (1 + (c_b + c)(d_b + d))\]また,コスト計算式において,攻撃力と会心系のみを考慮すると以下のような式になります.
\[\mathrm{cost}(\mathbf{x}) = \mathrm{cost}([a, c, d]) = 6.2\times \left(\frac{a}{0.047} + \frac{c}{0.031} + \frac{d}{0.062}\right)\]このとき,次の最適化問題を考えます.
\[\begin{align} &\text{maximize} &&\log f(\mathbf{x}) \\ &\text{subject to} &&\mathrm{cost}(\mathbf{x}) = S \end{align}\]この最適化問題の意味は,聖遺物のサブステータスの攻撃力%($a$)や会心率($c$),会心ダメージ($d$)が負の値を取ってもよいので, ダメージを最大化する最適な値を求める,という問題です. 負の値を取るというのは奇妙かもしれませんが,「真に最適にしたいなら,上げすぎたステータスを下げてでも足りないステータスに振りなさい」という意味であると理解していただけるとわかりやすいかもしれません. この問題はラグランジュの未定乗数法で解くことができます.
ラグランジュの未定乗数法より,ある定数$\lambda$について以下の二つの等式が同時に成立するときに最適です.
\[\nabla \log f(\mathbf{x}) = \lambda \nabla \mathrm{cost}(\mathbf{x}) \\ \mathrm{cost}(\mathbf{x}) = S\]上式の第一式はベクトルなので,それぞれ書き下すと,以下のようになります.
\[\begin{bmatrix} \frac{ A_\mathrm{b} }{ A_\mathrm{b} (1 + (a_b + a)) + A_\mathrm{add} } \\ \frac{(d_b + d)}{1 + (c_b + c)(d_b + d)} \\ \frac{(c_b + c)}{1 + (c_b + c)(d_b + d)} \\ \end{bmatrix} = \lambda \begin{bmatrix} \frac{6.2}{0.047} \\ \frac{6.2}{0.031} \\ \frac{6.2}{0.062} \end{bmatrix}\]つまり,会心率と会心ダメージのみを見れば以下の通りになります.
\[\begin{align} \frac{(d_b + d)}{1 + (c_b + c)(d_b + d)} &= \lambda \frac{6.2}{0.031} \\ \frac{(c_b + c)}{1 + (c_b + c)(d_b + d)} &= \lambda \frac{6.2}{0.062} \\ \end{align}\]上の二つの式の右辺の値はちょうど2倍になっていることと,左辺の分母が一致していることに注目すれば以下の式が得られます.
\[\begin{align} (d_b + d) = 2(c_b + c) \end{align}\]この式は,左辺は最終的な会心ダメージを表しており,右辺は最終的な会心率を表しています. 比率に関する式$x:y=v:w \Leftrightarrow xw = yv$を考えれば会心率と会心ダメージの比率が1:2になっており,つまりこれが最適比率であることがわかります.
[Tips] じゃあ攻撃力は?
では,次に疑問に思うのは,最適な攻撃力はいくつなのか,という話です. これも先程の等式を,つまり以下の式を$a$について解くだけです.
\[\frac{4.7}{3.1} \frac{ A_\mathrm{b} }{ A_\mathrm{b} (1 + (a_b + a)) + A_\mathrm{add} } = \frac{(d_b + d)}{1 + (c_b + c)(d_b + d)}\]上の式を整理して,左辺に攻撃力の最終ステータスが来るように式変形すれば以下の等式を得ます.
\[A_\mathrm{b} (1 + (a_b + a)) + A_\mathrm{add} = \frac{4.7}{3.1} \frac{1 + (c_b + c)(d_b + d)}{(d_b + d)} A_\mathrm{b}\]この式に会心率と会心ダメージの最適比率1:2を代入すると
\[A_\mathrm{b} (1 + (a_b + a)) + A_\mathrm{add} = \frac{4.7}{3.1} \frac{1 + 2(c_b + c)^2}{2(c_b + c)} A_\mathrm{b}\]たとえば会心率が$c_b + c = 0.6$(会心ダメージが$d_b + d=1.2$)ならば,
\[\begin{align} A_\mathrm{b} (1 + (a_b + a)) + A_\mathrm{add} \approx 2.17 A_\mathrm{b} && @ (c_b + c = 0.6) \end{align}\]となります. この意味は,会心率と会心ダメージがそれぞれ60%と120%なのであれば,攻撃力は基礎攻撃力の2.17倍程度まで盛ってもよい,という意味です. 他にはたとえば,会心率が20%のときは攻撃力は基礎攻撃力の約$4.09$倍,会心率が40%のときには基礎攻撃力の約$2.50$倍,会心率が80%のときには約$2.16$倍,会心率が80%のときには約$2.27$倍と変動します. というわけで,現実的にアタッカーの攻撃力は大体基礎攻撃力の$2.1$倍~$2.3$倍程度,つまり大体2000付近がちょうどよいと思っておけばいいでしょう(もちろん,胡桃やノエルのように攻撃力が盛れるキャラは例外です). 注意していただきたいのは,限られたリソース(コスト)を最大限に有効活用して最大のダメージ期待値を出すには,会心率と会心ダメージの比率が1:2がベストである,ことと同じく,会心率が60%~80%程度なのであれば攻撃力は2000付近でとどめておいて会心率・会心率ダメージへ割り振る方がよりダメージの期待値は大きくなるという意味です. また,会心率と会心ダメージの比率が1:2から外れるように会心ダメージを盛るのは意味がないわけではないことと同じく,攻撃力を2000以上盛る意味がないわけではありません. 逆に,攻撃力が2000付近に届いていないのにも関わらず,会心率と会心ダメージを盛ってもそれは最適解から外れています.
[Tips] ダメージバフはどれだけ盛ればいいの?
ダメージ計算式とコスト計算式にダメージバフを考慮して考えてみましょう. 聖遺物の杯において盛れるダメージバフは,(物理を除いて)全元素で46.6%です. これは攻撃力%の値と同じなため,コスト計算において攻撃力%のコストとダメージバフのコストは同じと考えられます.
すなわち,以下のようなダメージ計算式とコスト計算式を考えます. ここで,$g$がダメージバフの総量を表しています.
\[f(\mathbf{x}) = \{A_\mathrm{b} (1 + (a_b + a)) + A_\mathrm{add} \} (1 + (c_b + c)(d_b + d)) (1 + g)\] \[\mathrm{cost}(\mathbf{x}) = 6.2\times \left(\frac{a}{0.047} + \frac{c}{0.031} + \frac{d}{0.062} + \frac{g}{0.047} \right)\]今までと同じく,対数微分してラグランジュの未定乗数法を使えば,最適値において次の等式を得ます.
\[\frac{4.7}{3.1} \frac{1}{1 + g} = \frac{2(c_b + c)}{1 + 2(c_b + c)^2}\]これを$g$について式変形すれば以下の答えが出てきます.
\[g = \frac{4.7}{3.1} \frac{1 + 2(c_b + c)^2}{2(c_b + c)} - 1\]この式の意味を説明すると最もバランス良くステータスを盛るとすると,会心率が20%のときはダメージバフが約309%,会心率が40%のときには約150%,会心率が80%のときには116%,会心率が100%のときには127%が最もバランスの良いステータス配分である,ということです.
目指すべきステータスをまとめると,次のような表になります.
| 会心率% | 会心ダメージ% | 最終攻撃力/基礎攻撃力 | 合計ダメージバフ |
|---|---|---|---|
| 20% | 40% | 4.09倍 | 309% |
| 40% | 80% | 2.50倍 | 150% |
| 60% | 120% | 2.17倍 | 117% |
| 80% | 160% | 2.16倍 | 116% |
| 100% | 200% | 2.27倍 | 127% |
この表を見ると,会心率が60%~100%の広い範囲において,攻撃力は2.1倍~2.3倍程度,ダメージバフは110%~130%程度がバランスが良いことがわかります. というわけで,ダメージバフは110%~130%程度を目指しましょう.
ダメージの伸び率
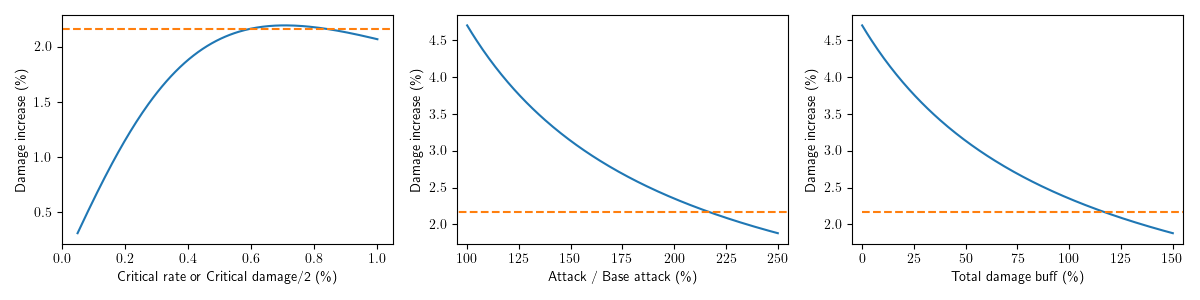
各ステータスに対するダメージの伸び率をグラフにすると以下の図になります. 以下の図では,聖遺物のサブステータスの1回の伸びに相当するダメージの上昇量を表示しています. つまり,たとえば会心率であれば3.1%増加したときに最終ダメージが何%増加するのかを表しています. ダメージバフについてはメインステータスで換算しており,つまりステータスの伸びる値は攻撃力%と同じだと換算しています. オレンジの点線は,会心率が60%のときのダメージの伸び値を表しています. このグラフを見れば分かる通り,攻撃力とダメージバフは単調減少関数ですが,会心率と会心ダメージは70%/140%付近で最大値を取る関数となっています.
聖遺物有効度
そのキャラクターに特定の武器と聖遺物をつけたときに,各サブステータスがどれだけダメージに影響を与えるかを考慮した数値です. 実際の計算は,サブステータスのみを無視してダメージ計算したときの勾配ベクトルから計算します. つまり,聖遺物のサブステータスベクトル$\mathbf{x}$に対してダメージ$f(\mathbf{x})$が計算できるとき,聖遺物有効度$E(\mathbf{x})$(Effectivity)は以下の通り計算できます.
\[E(\mathbf{x}) = \nabla \log f(\mathbf{0}) \cdot \mathbf{x} = \frac{\nabla f(\mathbf{0})}{f(\mathbf{0})} \cdot \mathbf{x}\]この式の意味は,そのキャラクターからサブステータスのみを抜き取ったときに,各サブステータスによるダメージの増加割合$\frac{\nabla f(\mathbf{0})}{f(\mathbf{0})}$と各サブステータスの量$\mathbf{x}$の内積で聖遺物有効度$E(\mathbf{x})$が計算できるということです. つまり,聖遺物有効度$E(\mathbf{x})$は各ステータスでどれだけダメージが増加するのかの割合になります. さらに言えば,聖遺物有効度$E(\mathbf{x})$にサブステータスを無視したダメージ$f(\mathbf{0})$を乗算すると(つまり,$E(\mathbf{x}) f(\mathbf{0})$),それはその聖遺物のサブステータスによってダメージがどれだけ増加するのかの目安になります. 注意として,この値は目安であって,実際の増加量ではないことに注意してください. つまり,以下の通りの近似関係が成立し,等式となるのは$\mathbf{x} \rightarrow \mathbf{0}$のときです.
\[f(\mathbf{x}) \approx (1 + E(\mathbf{x})) f(\mathbf{0})\]また,当たり前ですが,以下が成立することも聖遺物有効度$E(\mathbf{x})$を理解する上では重要です.
\[\nabla E(\mathbf{x}) f(\mathbf{0}) = \nabla f(\mathbf{0})\]聖遺物有効度は,全く同じ聖遺物でも,装備させるキャラクターや武器・聖遺物セットによって値が異なることに注意してください. つまり,一般的な聖遺物サブステータスのスコア計算式はどのキャラクターでも一律に計算してしまいますが,聖遺物有効度はキャラクターや武器によってどのステータスを伸ばすべきなのかという情報を反映した値です. しかしながら,聖遺物有効度は勾配ベクトル(微分値)を利用するため,目安の範囲を出ないことに注意してください. サブステータスが非常に大きい場合には近似が成立しませんから,万能なスコアではありません.
聖遺物の偏差値
聖遺物有効度や聖遺物スコアの確率分布がガウス分布に従うと仮定したとき,それぞれの値の偏差値を考えることができます. 聖遺物有効度やスコアがガウス分布に従うかについて疑問を持つ方が多いと思いますが,ある一定の仮定をすることでガウス分布だと考えることができます. まず,聖遺物のサブステータスは二項分布に従います. 二項分布は平均と分散がある程度あればガウス分布に近似できます. また,有効度やスコアが内積で計算されることに注目すると,つまりこれは複数の二項分布の和になっており,ガウス性をより強くします. 多少強引ですが,聖遺物有効度やスコアにはこのような性質があるためガウス性が生まれるでしょう.
以下の画像は1万回のシミュレーションによって聖遺物のスコアを算出したときのヒストグラムと,それと同一の平均値と分散を持つガウス分布の確率密度関数を表示しています. ただし,以下のことに注意してください.
- プログラムの都合上,聖遺物のサブステータスで攻撃力%と会心率と会心ダメージが上昇した回数のみをカウントしています.つまり,スコアは6.2で割って正規化しており,実際のスコアは横軸の値に6.2を掛けた値になります.
- プログラムでは上昇量は常に”中”のみで固定値になっています(というよりも,上昇した回数のみしかカウントしていません)ので,スコアの最大値も$8 \times 6.2 = 49.6$になっていることに注意してください.
- たとえば「メインステータスに攻撃力%がある聖遺物は,サブステータスに攻撃力%が付かない」というような仕様も無視していることに注意してください.
- シミュレーションに使用したプログラムの詳細はこちらから参照できます.
以下の図で,スコアが0の聖遺物が多い理由は,今回は攻撃力%と会心率と会心ダメージしか考慮しないスコア計算なため,もともとこれらの三つのサブステータスが一つもついていない聖遺物はどれだけ強化してもスコアは0のままなためです. 一方で,三つのサブステータスのうち一つでも最初から付いていれば,強化によってスコアは上昇する可能性があるため,ヒストグラムの隣のビン(スコアが$1 \times 6.2 = 6.2$)は少なくなっています. スコア0の部分が大きく外れていますが,それ以外の部分では大まかにガウス分布に近似できそうなことがわかります.
ちなみに,平均スコアは$2.69 \times 6.2 = 16.7$であり,標準偏差は$\sqrt{3.69} \times 6.2 = 11.9$です. そのため,スコアが$16.7 + 11.9 = 28.6$の聖遺物の偏差値が60になります. 同様に,偏差値70の聖遺物スコアは40.5であり,偏差値80の聖遺物スコアは52.4になります. 聖遺物のスコアが$X$のとき,偏差値の計算式は次のとおりです.
\[\text{聖遺物スコア偏差値}(X) = 50 + 10 \times \frac{X - 16.7}{11.9} \approx 50 + 10 \times \frac{X - 17}{12}\]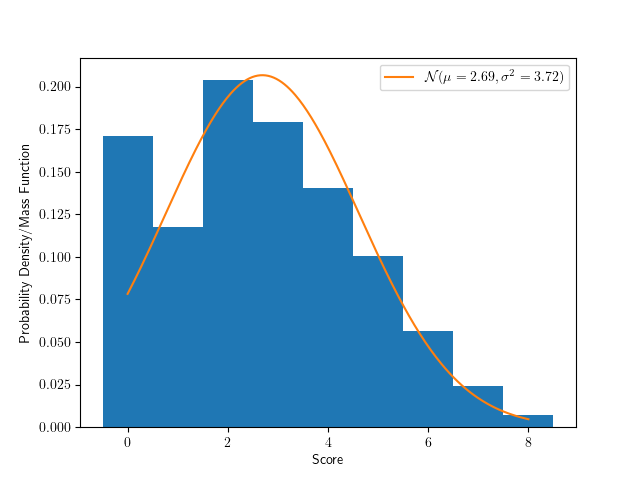
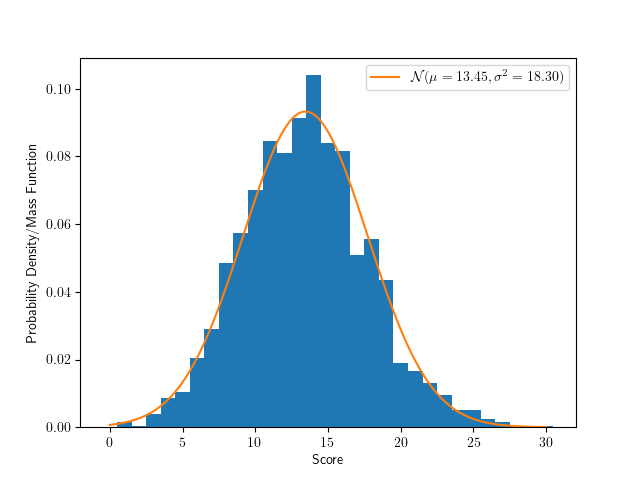
以下の図は,5部位の聖遺物のスコアの和のヒストグラムと,それと同一の平均値と分散を持つガウス分布の確率密度関数を表示しています. 5部位の聖遺物スコアの和の分布は,非常に綺麗にガウス分布に近似できそうです.
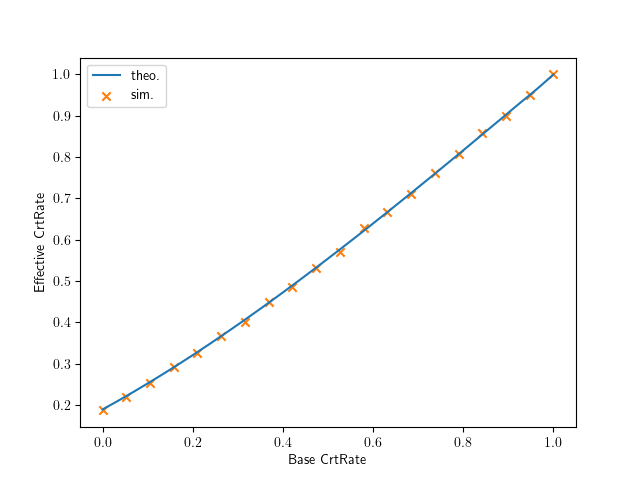
旧貴族武器の会心率について
旧貴族武器は,会心が出るまで無凸でも最大で会心率が+40%される,一見すごく優秀な武器です. しかしながら,実際には「会心が出るまで会心率が上昇する」ため,もともと高い会心率のキャラクターにとっては全く恩恵はありません. では実際にどれだけ会心率が上昇するのか計算しましょう. キャラクターのもともとの会心率を$p$,旧貴族武器での会心率の上昇分を$x$とします. 各攻撃の会心率と発生確率は次のとおりです. ただし,以下の箇条書きで「4回目」とは「過去3回ともに会心が出なかったときの4回目の攻撃」を意味します. また,$n$回目での会心率を表す変数を$p_n = \mathrm{min}(p+nx, 1)$とします.
- 1回目で会心になる確率$p_0$,会心にならない確率$1-p_0$
- 2回目で会心になる確率$(1-p_0)p_1$,ならない確率$(1-p_0)(1-p_1)$
- 3回目で会心になる確率$(1-p_0)(1-p_1)p_2$,ならない確率$(1-p_0)(1-p_1)(1-p_2)$
- 4回目で会心になる確率$(1-p_0)(1-p_1)(1-p_2)p_3$,ならない確率$(1-p_0)(1-p_1)(1-p_2)(1-p_3)$
- 5回目で会心になる確率$(1-p_0)(1-p_1)(1-p_2)(1-p_3)p_4$,ならない確率$(1-p_0)(1-p_1)(1-p_2)(1-p_3)(1-p_4)$
- 6回目で会心になる確率$(1-p_0)(1-p_1)(1-p_2)(1-p_3)(1-p_4)p_5$,ならない確率$(1-p_0)(1-p_1)(1-p_2)(1-p_3)(1-p_4)(1-p_5)$
- 7回目で会心になる確率$(1-p_0)(1-p_1)(1-p_2)(1-p_3)(1-p_4)(1-p_5)p_5$,ならない確率$(1-p_0)(1-p_1)(1-p_2)(1-p_3)(1-p_4)(1-p_5)^2$
- $X$回目($X \geq 6$)で会心になる確率$(1-p_0)(1-p_1)(1-p_2)(1-p_3)(1-p_4)(1-p_5)^{X-6}p_5$,ならない確率$(1-p_0)(1-p_1)(1-p_2)(1-p_3)(1-p_4)(1-p_5)^{X-5}$
会心率とは会心が発生するまで何回攻撃したかの逆数なので,実質的な会心率$P$は次の通りです.
\[P = \left\{p_0 + 2(1-p_0)p_1 + 3(1-p_0)(1-p_1)p_2 + 4(1-p_0)(1-p_1)(1-p_2)p_3 + 5(1-p_0)(1-p_1)(1-p_2)(1-p_3)p_4 + (1-p_0)(1-p_1)(1-p_2)(1-p_3)(1-p_4)p_5\sum_{n=6}^{\infty} n(1-p_5)^{n-6} \right\}^{-1}\]ちなみに,最後の級数の部分は以下の通りです.
\[\sum_{n=6}^{\infty} n(1-p_5)^{n-6} = \sum_{n=0}^{\infty} (n+6)(1-p_5)^{n} = \frac{1 + 5p_5}{p_5^2}\]以下の図は,理論で導出した実質的な確率と,1万回のシミュレーション結果です. まあまあシミュレーション結果と合っているので良しとしてください. ちなみに,プログラムの詳細はこちらから参照できます.
来歆の余響4セット効果の実質的な発動確率
旧貴族武器と同じようにして,来歆の余響4セット効果の実質的な発動確率を計算できます. $p_0=0.36, p_1=0.56, p_2=0.76, p_3=0.96, p_4=1$とすれば,実質的な発動確率$P$は以下の通りです.
\[P = \left\{p_0 + 2(1-p_0)p_1 + 3(1-p_0)(1-p_1)p_2 + 4(1-p_0)(1-p_1)(1-p_2)p_3 + 5(1-p_0)(1-p_1)(1-p_2)(1-p_3)p_4 \right\}^{-1}\]これを計算すると,$P=0.502$となり,約50%の確率で実質的には発動することを意味します.